코세라 앤드류 응 교수님의 딥러닝 1번째 코스, 신경망 및 딥러닝 코스의 4주 차 강의 내용 리뷰입니다.
이번 시간에는 L층으로 구성된 심층 신경망(Deep L-layer Neural Networks)에 대해 배워봅시다.

What is a deep neural network?

딥러닝에서 층(Layers)의 개수를 말할 때는,
보통 입력층을 제외한 결과층과 은닉층의 수만을 이야기 합니다.
예를 들어, 위의 그림의 신경망 수는 각각 1층, 2층, 3층, 6층인 것이죠.
무조건 층이 겹겹이 많이 쌓였다고 해서 좋은 것은 아니지만,
우리가 해결하고자 하는 현실의 복잡한 문제들은 "비선형 문제"이기에,
보통은 층이 깊으면 깊을수록 문제를 더 효과적으로 해결할 수 있습니다.
*주의 ) 그렇다고 층의 수가 너무 많으면, 학습 시간이 너무 길어지거나 과적합(Overfitting)의 문제가 생길 수도 있기에,
각각의 상황에 따라 적절한 층의 수나 매개변수를 설정하는 것이 중요합니다.
Deep neural network notation
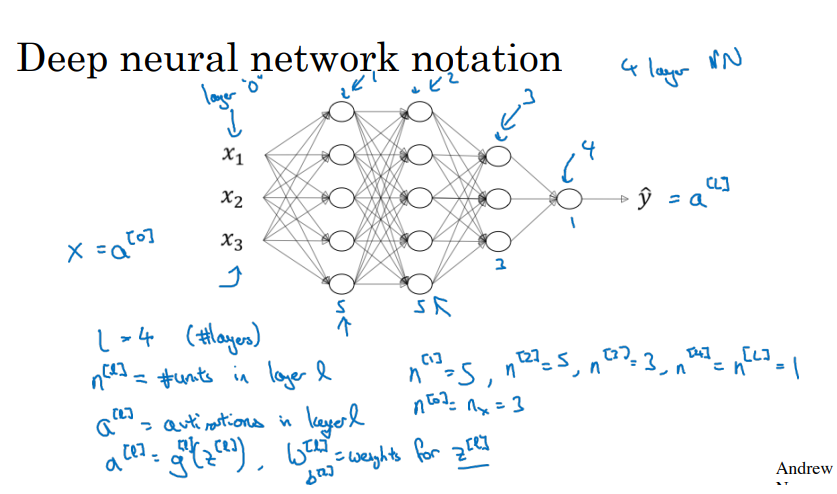
신경망에서 쓰이는 표현들을 알아보겠습니다.
위의 신경망은 4개의 층으로 구성되어 있으며,
입력 데이터는 a [0]이라고 표현하며, 입력층은 따로 계산하지 않습니다.
오른쪽부터 1~4층으로 표현하며,
처음의 입력 데이터 X는 각각의 퍼셉트론에 입력될 때, 각각 다른 가중치 w를 곱하고
각각의 퍼셉트론마다 가지는 고유의 값인 편향 b를 더한 후,
참고)
가중치 w는 신경망을 잇는 선을 나타내기에 각각 다른 값이지만,
편향 b는 퍼셉트론(하얀색 동그라미)에 입장하기 위한 입장료의 개념이기에,
같은 퍼셉트론에 연결된다면 편향 b는 모두 같습니다.
모두 더해져서 Z로 표현되고 , 활성화 함수 g의 입력 값이 됩니다.
그리고, 계산되어 나오는 활성화 함수의 출력 값인 a [?]가 다음 층의 입력 값이 되는 방식입니다.
각각의 층마다 저런 과정을 거치며, 최종적으로 예측치 y-hat이 산출되는 것이 심층 신경망 학습에서의 순전파 계산입니다.
Forward Propagation in a Deep Network

심층 신경망 학습(=딥러닝)의 학습 과정은 크게 2가지 단계로 이루어집니다.
1단계 - 순 전파(Forward Propagation) 단계
이 단계에서는 입력된 데이터가 각각의 신경망 층을 지나치며,
결과적으로 데이터에 대한 기계의 예상치인 Y-hat을 산출하는 과정입니다.
2단계 - 역전파(Backward Propagation) 단계
이 단계는, 1단계에서 산출된 Y-hat을 통해서 나온 (결과와 예상의 차이를 의미하는) 손실(loss) 값을 통해서,
손실(loss)을 최소화하는 좋은 방법인경사 하강법(Gradient Descent)을 사용하여 매개변수 w , b를 수정하는 단계입니다.
경사 하강법을 통해서 매개변수를 수정함으로써, 손실(loss)은 점점 작아지게 됩니다.
참고)경사 하강법(Gradient Descent)은 활성화 함수의 미분 값을 이용하여, 손실을 최소화하는 방향을 찾는 방법입니다.
결국, 딥러닝의 학습 목적은 적절한 매개변수 W, b의 값을 찾아 수정함으로써, 가장 낮은 손실을 만드는 것이 목적입니다.
--> 가장 낮은 손실(loss)은 정답과 딥러닝 모델의 예측이 비슷하다는 뜻이니, 가장 정확하다는 의미입니다.
Forward propagation in a deep network

이 중에서, 1단계인 순 전파(Forward Propagation) 과정을 수학적으로 표현해보겠습니다.
벡터(Vetor)를 이용하여 표현했는데, 벡터(vetor)를 이용하여 신경망을 계산하면 훨씬 편리하게 나타낼 수 있습니다.
예를 들어서, 1층에 있는 5개의 퍼셉트론들을 벡터(행렬)로 묶어서 한 번에 연산하게 되면, 계산과정을 훨씬 간단하게 나타낼 수 있게 됩니다.
(이전 3주 차 포스팅 참고) 또한, 계산과정이 간편해져서, 실제 학습 시간을 단축시킬 수 있습니다.
Z [1] = W [1] * a [0] + b [1]부터 살펴보겠습니다.
Z [1]는 1층에서의 (가중치 w와 입력치 a의 곱 + 편향 b)을 나타내는데, 활성화 함수의 입력치를 의미합니다.
W [1]은 입력 데이터~1층 사이의 가중치 w를 모아논 벡터(=배열, 행렬)이며,
a [0]은 입력 데이터 x들을 모아논 벡터이며,
b [1]은 1층의 퍼셉트론들의 편향 b를 모아논 벡터입니다.
A [1]는 1층에서의 활성화 함수의 결괏값들을 모아논 벡터(=배열, 행렬)입니다.
이 값은 다시 a [1]으로, 다음 층인 2층의 입력값이 되는 것이죠.
이렇게 층을 거쳐서, 결국 마지막에 산출되는 값인 a[4]가 예상치인 Y-hat가 됩니다.
오늘은 저번 시간의 내용을 복습하며, 간단하게 L층을 가진 심층 신경망이 어떤식으로 구성되는지 알아보았고,
이상으로 4주차 첫번째 시간을 마치도록 하겠습니다.
다음 시간에는,
딥러닝 학습과정에서 이루어지는 행렬의 연산과정에서, 행렬의 차원수는 어떠한지 알아보겠습니다.
이 내용들은 모두 coursera에서 앤드루 응 교수님의 강의를 요약정리 및 쉽게 재 풀이하여 적은 글이며,
내용에는 생략되거나 변형된 부분이 많으니 직접 강의를 들어보시는 걸 추천드립니다!
이 글은 상업적 목적이 아닌, 한국에서 인공지능을 배우고 싶은 분들을 위해 적은 교육적 목적에서 작성하였습니다
'코세라 앤드류 응 AI 강의 리뷰' 카테고리의 다른 글
| [인공지능 강의 리뷰] 24 - 심층 신경망에서의 순전파(forward propagation) + 역전파(back propagation) (0) | 2022.07.16 |
|---|---|
| [인공지능 강의 리뷰] 23 - 왜 신경망의 층을 깊게하는 걸까? ( why deep repretations?) (0) | 2022.07.05 |
| [인공지능 강의 리뷰] 22 - 딥러닝에서 행렬의 크기 알아보기(Getting your matrix dimensions right) (0) | 2022.06.01 |
| [인공지능 강의 리뷰] 20 - 하나의 숨겨진 레이어를 사용한 평면 데이터 분류. 프로그래밍 과제 (0) | 2022.05.19 |
| [인공지능 강의 리뷰] 19 - 하나의 숨겨진 레이어를 사용한 평면 데이터 분류. 프로그래밍 과제 (0) | 2022.05.18 |
| [인공지능 강의 리뷰] 18 - 하나의 숨겨진 레이어를 사용한 평면 데이터 분류. 프로그래밍 과제 (2) | 2022.05.17 |
| [인공지능 강의 리뷰] 17 - 총정리 퀴즈. 얕은 신경망(Shallow Neural Network) (0) | 2022.05.17 |