3 - General Architecture of the learning algorithm

각각의 픽셀의 값들은 (RGB 색깔의 세기 값을 나타내는) 0~255 값이 적혀있습니다.
기계 학습의 일반적인 전처리 단계 중 하나는, 데이터 세트를 중앙에 배치하고 표준화하는 것입니다.
원래는 각 예제에서 전체 행렬(배열)의 평균을 뺀 다음 각 예제를 전체 행렬(배열)의 표준 편차로 나눕니다.
하지만 저희가 훈련하는 사진 데이터 세트의 경우,
데이터 세트의 모든 행을 255(픽셀 채널의 최댓값)로 나누는 것이 더 간단하고 편리하며 거의 잘 작동합니다.
기억해야 할 점 :
새 데이터 세트를 사전 처리하는 일반적인 단계는 다음과 같습니다.
-문제의 크기와 모양을 파악합니다(m_train, m_test, num_px,...).
-각 예제가 (num_px * num_px * 3, 1)의 벡터가 되도록 데이터 세트의 형태를 변경합니다.
-데이터 "표준화"합니다. --> 255로 나누기


위의 그림은, 로지스틱 회귀를 이용한 뉴럴 네트워크를 아주 쉽게 설명하는 그림입니다.
중요한 단계 : 이 연습에서는 다음 단계를 수행합니다.
- 모델의 매개변수 초기화
- 비용을 최소화하여, 모델의 매개변수 학습
- 학습된 매개변수를 사용하여 테스트 세트에서 예측
- 결과 분석 및 결론
4 - Building the parts of our algorrithm
+ 4.1 - Helper functions ( Exercise 3)

신경망(Neural Network)을 구축하기 위한 주요 단계는 다음과 같습니다.
모델 구조 정의(예: 입력 특징의 수)
모델의 매개변수 초기화
loop(반복) :
1 - 현재 손실 계산(순방향 전파, forward Propagation)
2 - 현재 기울기 계산(역전파, Backward Propagation)
3 - 매개변수 업데이트(경사 하강법, Gradient descent)
종종 1~3을 별도로 분리하거나 model()이라고 하는 하나의 함수로 통합합니다.
Python 코드를 사용하여 sigmoid()를 구현합니다.
위 그림에서 보았듯이 𝑧=𝑤𝑇𝑥+𝑏에 대해 np.exp() 사용하여, 𝑠𝑖𝑔𝑚𝑜𝑖𝑑(𝑧)를 계산해야 합니다.

리턴 값으로 sigmoid(z)가 나와야 하니,
시그모이드 함수(sigmoid function)를 코드로 정의해 주어야 합니다.

np.exp() 코드로 자연로그 e를 표현하여 입력해 줍시다.
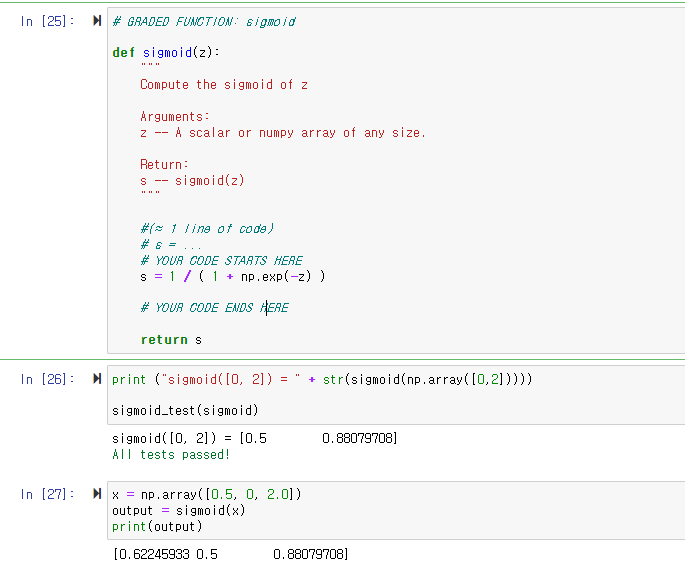
실행하면, 정답인 걸 확인할 수 있습니다. 다음으로 넘어가 봅시다.
4.2 - Initializing parameters (Exercise 5)
initialize_with_zeros()는 매개변수를 초기화 한 값을 반환합니다.
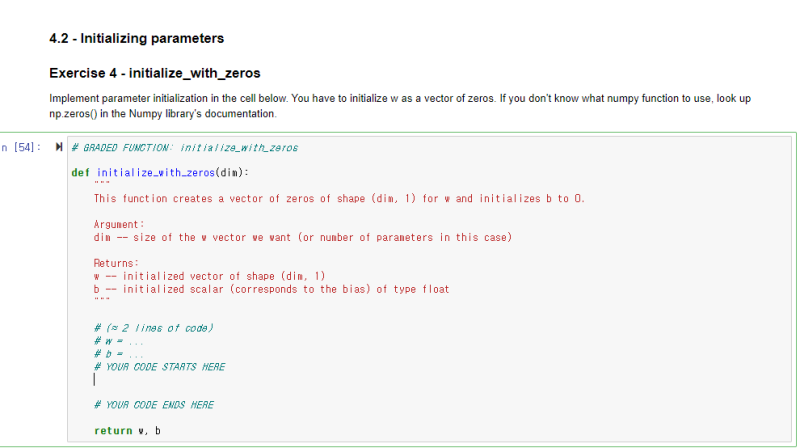
np.zeors()를 매개변수를 초기화해야 합니다.
--> np.zeros( A)는 0으로 구성된 A 차원의 행렬(배열)을 반환하는 numpy 함수입니다.
리턴 값으로, w는 dim * 1 행렬(배열) , b는 실수 타입 0이 나와야 합니다
주의할 점은 b는 실수 타입이기에, 0이 아닌 0.0으로 나타내야 합니다!

코드를 작성하고, 실행해 봅시다.

실행해 보면, 성공적으로 결과가 나온 걸 확인할 수 있습니다!
4.3 - Forward and Backward propagation (Exercise 5)

이제 매개변수를 초기화하기 위해서, 손실 함수와 기울기를 계산해야 합니다.
아래의 propagate()는 비용 함수와 기울기를 반환합니다

저희가 작성해야 할 코드는 총 4줄입니다!
(활성화 함수, 비용 함수, w에 대한 비용 함수의 미분 값, b에 대한 비용 함수의 미분 값)

w.T * X는 행렬의 곱이므로, np.dot()을 사용하고,
시그마 기호로 나타낸 총합은 np. sum()으로 표현해서 나타내면 됩니다.

dw와 db 또한 그대로 코드로 옮겨서 작성하기만 하면 됩니다.

코드를 작성하면 이렇게 됩니다!

실행하여 정답을 확인했으니 , 다음으로 넘어가 봅시다.
4-4 Optimization (Exercise 6)

매개변수를 초기화했습니다.
이제 비용 함수와 그 기울기를 계산할 수도 있습니다.
경사 하강법을 사용하여 매개변수를 업데이트해봅시다.
목표는 비용 함수를 최소화하는 𝑤 과 𝑏 를 알아내는 것입니다.
매개 변수의 경우 업데이트 규칙은 𝜃=𝜃−이며, 여기서 𝛼은 학습률입니다.
이제 optimize() 최적화 함수를 정의해 봅시다.
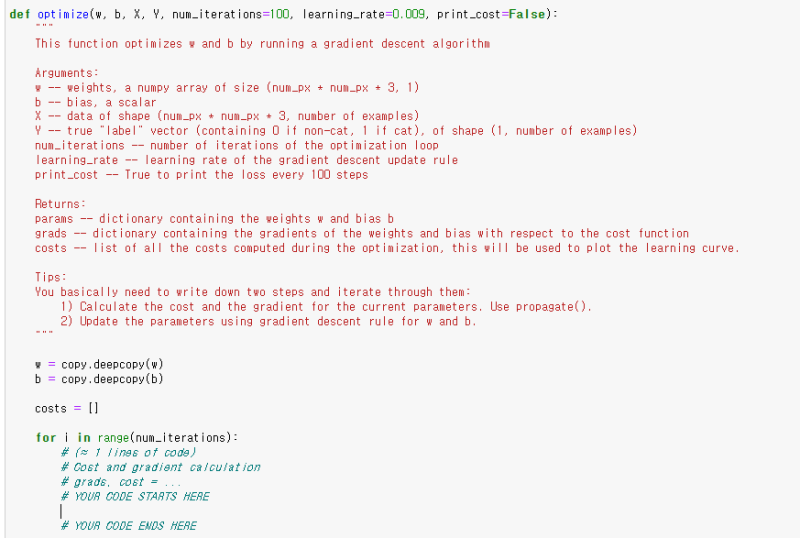

grads , cost는 바로 직전 propagate()로 구현했으니, 불러만 주면 됩니다!
w, b도 문제에서 dw, db가 정의돼있으니 학습률(learning late)만 곱해서 작성해 주면 됩니다.

이렇게 코드를 작성하면 됩니다! 정답인지 확인해 봅시다.

정답인 걸 확인했습니다!
매개변수를 업데이트하는 과정까지 다 끝냈습니다.
훈련 모델을 다 만들었으니, 다음 글에 이어서
만든 로지스틱 회귀 모델을 테스트 데이터를 통해서 테스트해봅시다.
이 내용들은 모두 coursera에서 앤드루 응 교수님의 강의를 요약정리 및 쉽게 재 풀이하여 적은 글이며,
내용에는 생략되거나 변형된 부분이 많으니 직접 강의를 들어보시는 걸 추천드립니다!
이 글은 상업적 목적이 아닌, 한국에서 인공지능을 배우고 싶은 분들을 위해 적은 교육적 목적에서 작성하였습니다.
'코세라 앤드류 응 AI 강의 리뷰' 카테고리의 다른 글
| [인공지능 강의 리뷰] 16 - 왜 활성화 함수에 비선형 함수를 써야할까? (0) | 2022.05.17 |
|---|---|
| [인공지능 강의 리뷰] 15 - 뉴럴 네트워크 And 벡터화 표현 (0) | 2022.05.17 |
| [인공지능 강의 리뷰] 14 - 프로그래밍 과제 . 신경망 사고방식을 이용한 로지스틱 회귀 모델 만들기3 (고양이 사진 분류기) (0) | 2022.05.16 |
| [인공지능 강의 리뷰] 12 - 프로그래밍 과제 . 신경망 사고방식을 이용한 로지스틱 회귀 모델 만들기 (고양이 사진 분류기) (0) | 2022.05.16 |
| [인공지능 강의 리뷰] 11 - 신경망 기초 테스트 (Neural Network Basic Quiz) (0) | 2022.05.16 |
| [인공지능 강의 리뷰] 10 - 브로드캐스팅(Broadcating in Python) (0) | 2022.05.16 |
| [인공지능 강의 리뷰] 9 - 벡터화(Vectorization) (0) | 2022.05.16 |