
저번 시간에 이어서,
도함수(Derivative) 와 계산 그래프(Computation Gragh)에 대해 알아봅시다.

도함수(Derivative)는 어떤 함수 a의 접선의 기울기를 나타내며, 미분(Differential)과 같은 뜻입니다.
접선의 기울기란, 어떤 지점에서 x의 순간 변화량에 대한 y의 순간 변화량을 나타냅니다.
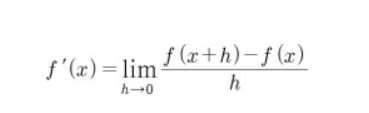
수학적 정의는 위의 그림과 같습니다.
f(x)의 도함수는 f'(x)로 나타냅니다.

다시 강의 자료로 돌아가 봅시다.
예를 들어서, f(a) = 3a라는 함수가 있다고 가정하겠습니다.
쉬운 이해를 위해서 a = 2 , h = 아주 작은 수 0.001 이라고 하겠습니다.
도함수의 정의에 의해서, f'(2) = { f (2+0.01) - f (2) } / 0.001 ,f'(2) = ( 6. 003 - 6 ) / 0.001 = 3 이고,
f'(5) = (15.003 - 15) / 0.001 = 3입니다.
이것을 일반화하면, { 3(a+h) - 3a } / h = 3 , f'(a) = 3 이 됩니다.


마찬가지로,
f'(a) = {(a+h)'2 - a'2} / h = 2a + h = 2a -->( h는 0에 한없이 가까우므로)
f(a)의 도함수는 2a가 됩니다.

간략하게 도함수(Derivative)를 짚어보았고, 바로 이어서
계산 그래프( Computation Graph)은 어떤 식으로 이뤄지는지 알아봅시다
.
--> 신경망 ( 딥러닝)에서의 계산은 순방향(순천 파) 과 역방향(역전파)로 구성되는데,
각각 왜 사용하는지 차이를 계산 그래프(Computation Gragh)를 통해 확인해 봅시다.
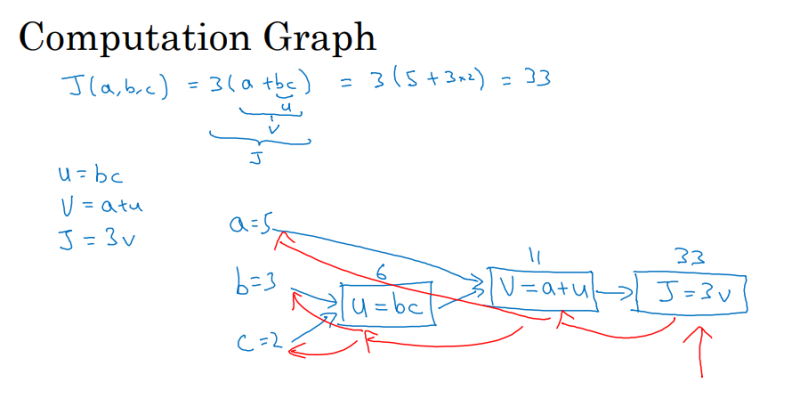
예를 들어서, 컴퓨터가 J(a, b, c) = 3 ( a+bc)라는 함수를 계산한다고 가정해 봅시다.
a = 5 , b = 3 , c =2라고 하면,
가장 1번째로, b*c를 계산하여 어떤 곳(u)에 그 값을 저장합니다.
그리고, u 안에 들어있는 값 ( = 6) 과 a의 값을 더해서, 어떤 곳 (v)에 저장합니다
마지막으로, v 안에 들어있는 값 (= 11)과 3을 곱해서 J에 넣어주어 계산을 끝냅니다.
위 방식과 같은, 순방향 방식은 함숫값을 구하는데 사용하며,
뒤에 나올 역방향 방식은 미분 값을 구하는데 사용합니다.

계산 그래프(Computation Gragh)에서, 역방향 계산을 이용하여 미분 값을 구해봅시다.
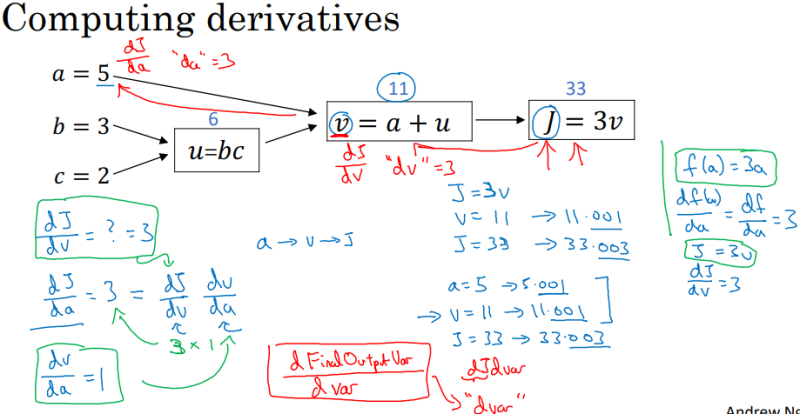
도함수 계산의 경우,
왼쪽에서부터 - > 오른쪽이 아닌,
오른쪽에서부터 -> 왼쪽으로 계산합니다
오른쪽 끝에서부터 계산해 봅시다.
도함수의 정의에 의해서, dJ / dv = 3 이 됩니다.
-----> 강의에서는 이 값들을 ( dj / dv)를 문자 이름 dv에 넣어준다고 표현하였고,
(dj / db)를 db (dj / da)를 da로 표현했습니다.
보기에 굉장히 헷갈리기에, 저는 dj / db로만 표현하였습니다!
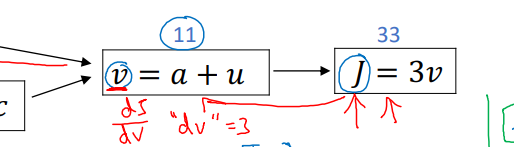
v = a + u로 넘어가 봅시다.
v(a) = a+ u라고 생각하여, a로 양변을 미분하면 dv / da = 1 됩니다.
저희가 구하려는 건 J에 관한 도함수 dj / da이기에, 분모 분자에 dj를 곱해줍시다.
그러면, ( dv / dj) * ( dj / da) = 1 이 됩니다.
처음에 dj / dv = 3이라고 구했기에 계산하면, dj / da = 3 * 1 = 3 이 됩니다.
v = a + u를 v(a)로 볼 때와 동일하게, v(u)로 보고 미분하면 dj / du = 3이 됩니다.
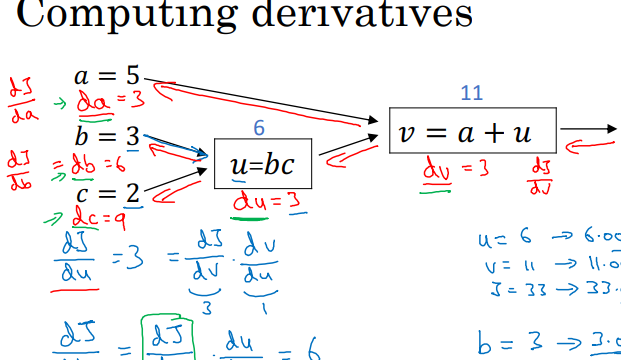
u = bc를 계산해 봅시다.
저번과 마찬가지로, u(b) = bc로 보면, du / db = c / db입니다.
du / db = c가 되고 , du / dc = b 가 됩니다.
분모 분자를 dj로 나눠주면, (du / dj) / ( db / dj) = c , (du / dj) / (dc /dj) = b 가 됩니다.
b = 3 , c = 2이기에, 위에서 구했던 dj / du = 3을 대입하여 계산해 주면,
dj / db = 2 * 3 = 6 , dj / dc = 3* 3 = 9 가 됩니다.
다음 시간에서는, 신경망에서 경사하강법을 사용하기 위해서 필요한 도함수를 계산해보겠습니다!
이 내용들은 모두 coursera에서 앤드루 응 교수님의 강의를 요약정리 및 쉽게 재풀이 하여 적은 글이며,
내용에는 생략되거나 변형된 부분이 많으니 직접 강의를 들어보시는 걸 추천드립니다!
이 글은 상업적 목적이 아닌, 한국에서 인공지능을 배우고 싶은 분들을 위해 적은 교육적 목적에서 작성하였습니다.
'코세라 앤드류 응 AI 강의 리뷰' 카테고리의 다른 글
| [인공지능 강의 리뷰] 10 - 브로드캐스팅(Broadcating in Python) (0) | 2022.05.16 |
|---|---|
| [인공지능 강의 리뷰] 9 - 벡터화(Vectorization) (0) | 2022.05.16 |
| [인공지능 강의 리뷰] 8 - 로지스틱 회귀 경사 하강법(Logistic Regression Gradient Descent) (0) | 2022.05.16 |
| [인공지능 강의 리뷰] 6 - 경사 하강법(Gradient Descent) (0) | 2022.05.09 |
| [인공지능 강의 리뷰] 5 - 로지스틱 비용 함수(Logistic Regression Cost function) (0) | 2022.05.02 |
| [인공지능 강의 리뷰] 4 - 로지스틱 회귀(Logistic Regression) (0) | 2022.05.02 |
| [인공지능 강의 리뷰] 3 - 이진 분류(Binary Classification) 와 로지스틱 회귀(Logistic Regression) (0) | 2022.05.02 |